数学和音乐有着直接、多层、深入的关联,从物理发声的原理到群论等,跨越应用数学和理论数学、音乐的演奏和音乐的理论,从音乐理论家勋伯格到数学家丘成桐、王杰等已多有研究。音乐的计算机视觉呈现可以理解为数学艺术(mathematical art)的一种。音乐研究中的可视化案例并不鲜见,但将音乐的审美直觉和数学规律结合的呈现仍然是较有挑战的问题。作品尝试以计算机艺术平衡前者的传达效率,与后者的表现深度。
这是一件结合计算机艺术的表现方法,以巴赫( Johann S. Bach)的《哥德堡变奏曲》(Goldberg Variations)(BMW. 988)的首曲咏叹调(Aria)为例,研究音乐与数学关系的作品,尝试将“时间”和“音乐中的建筑结构”具象化,也是一个持续拓展的研究项目。作品采用了音频、乐谱两种数据导入方式,分别对应直觉、理性的信息接收途径,形成了在音乐背景中旋转的金色旋律塔(Rhythm Tower)和音符连线数据柱两个三维模型,呈现了将审美从听觉到视觉的转译尝试,以及对巴赫作曲规律的观察,亦是关于何为“美”的认知和哲学探讨。
本作品的旋律塔部分曾于美国数学联席会议展览展出(图1、2)。巴赫的乐曲以数学性著称,而《哥德堡变奏曲》由 32 段组成,正好对应咏叹调的 32 个小节,是其代表性的结构恢宏、对称繁复巧妙的作品,而目前的视觉生产仅探索了统摄全组曲的首段咏叹调,后续曲目可形成完整的虚拟建筑群落,富有研究和创作潜力。
图1
图2
旋律塔部分(图3、4)是由音频中的音高和音速数值编织而成的,形状设计对应巴赫音乐中常见的盘旋上升之感,绿-金-橙色渐变的旋转模型的编织折线在模拟光源下渐次闪亮、变暗,模拟其蕴藉典雅的风格。音频数据并不能直接分开同一种乐器的高低声部和小节隔断,更多地反映了聆听的直接感受。32 小节按照明显的休止符间隔被分为 4 层,按时间由下而上。每条线段代表一个音符,线段斜度由音高决定,颜色由时间和音高共同决定。旋律塔每层的边缘部分由该段音符的音速组成。咏叹调的尾部最为活跃,线条的跳跃性也最大。

图3

图4
数据柱部分(图5,6)是由乐谱(图7,8)直接编写生成的,也是旋转的三维模型,体现了巴赫用当时流行的以低音线为基准作曲的方法,更为准确和直接地表达了时间、低音线、高声部主曲的关系,以及不同部分的对称、旋律模型的重复(如低音线的前后半段为重复关系)。为查看方便,本文图示未加入装饰音等,完整的模型细节更为复杂。
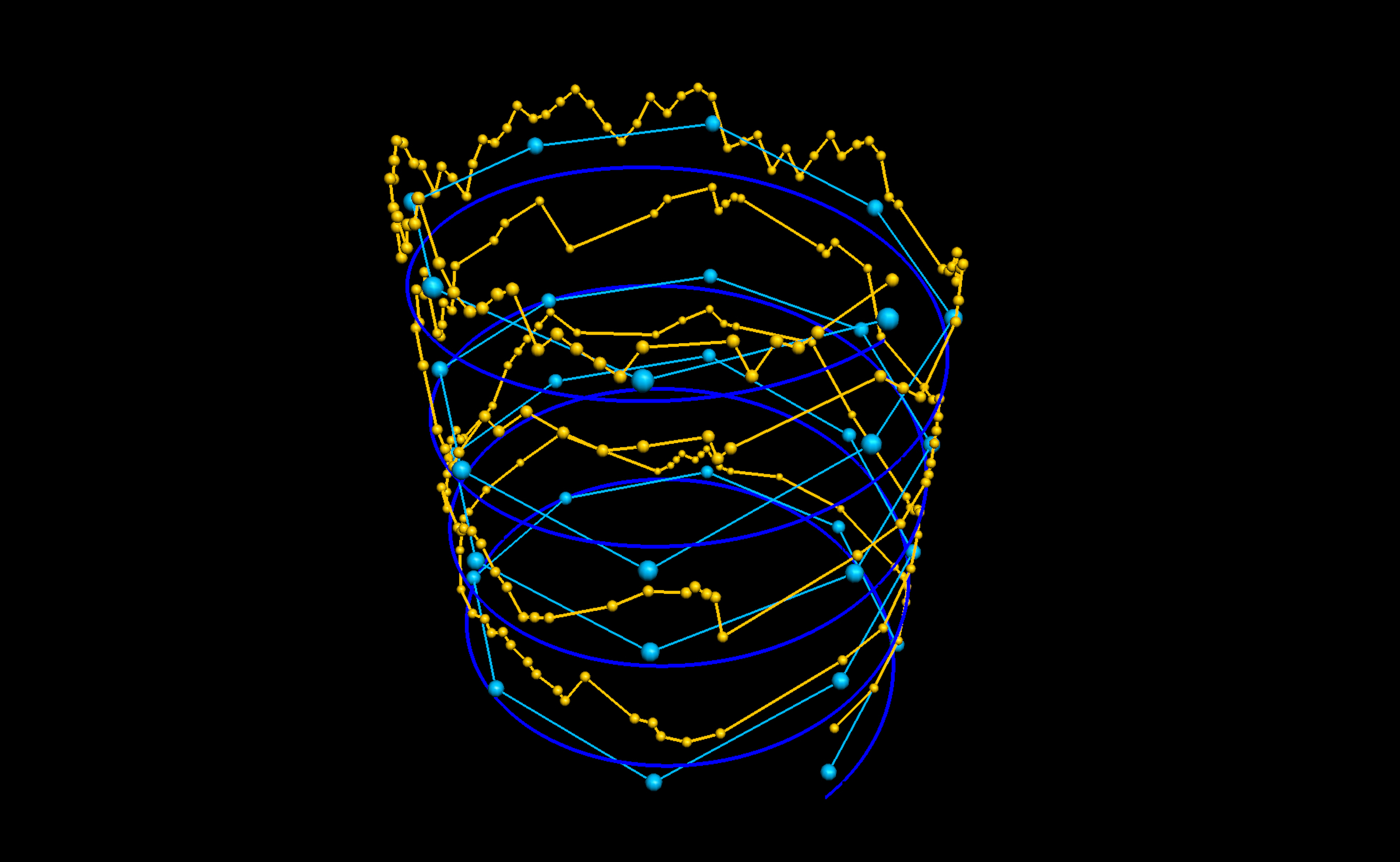
图5

图6
同前部分,构图随时间流逝由下而上。深蓝色螺旋曲线代表时间。浅蓝色折线为低音基准线,浅蓝色圆球代表每小节的分隔,也是 32 个低音的具象化。黄色线条为高声部,黄色小球代表的音符由折线连接。以数据柱细节图为例,这个模型能比较直接地观察到高声部旋律和低音基准线的变化关联规律,以及以每小节左右的长度为单位的旋律模式重复规律。

图7

图8
作者简介:
周融荣,博士,评论和策展人,世界华人科幻协会会员。任职于北京大学,助理研究员。关注计算机艺术、科技美学、科学传播、文化产业。毕业于香港科技大学数学系(BS)、苏富比艺术学院(伦敦)东亚艺术史专业(MS)、中央美术学院(Ph.D)。在中国美术馆等处独立策展,参与国家艺术基金项目。曾于 ICBC 集团等任宏观和投资分析、私人银行艺术顾问、美术馆策划总监。从事计算机艺术/评论/小说/诗歌创作,以中/英/德/西语见诸海内外,如美国数学联席会议(JMM)展览、哈佛燕京学社、人文社科核心期刊等。获科幻“光年奖”等。
